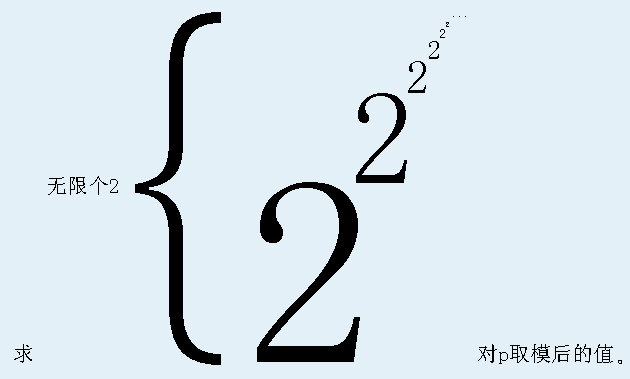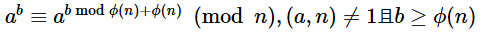上帝与集合的正确用法

Time Limit: 5 Sec Memory Limit: 128 MB

Description

img

Input

第一行一个T，接下来T行，每行一个正整数p，代表你需要取模的值。

Output

T行，每行一个正整数，为答案对p取模后的值。

Sample Input

3
　2
　3
　6

Sample Output

0
　1
　4

HINT

对于100%的数据，T<=1000，p<=10^7

Solution

我们运用欧拉定理：

img

然后还有一个定理：一个数在执行log次操作后，值不会改变。

然后就可以直接求了。

Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
#include<bits/stdc++.h>
using namespace std;
typedef long long s64;

const int ONE = 500005;
const int INF = 2147483640;

int T,x;
int phi[ONE],pn;

int get()
{
    int res=1,Q=1;char c;
    while( (c=getchar())<48 || c>57 )
        if(c=='-')Q=-1;
    res=c-48;
    while( (c=getchar())>=48 && c<=57 )
        res=res*10+c-48;
    return res*Q;
}

int Quickpow(int a,int b,int MOD)
{
    int res = 1;
    while(b)
    {
        if(b & 1) res = (s64)res * a % MOD;
        a = (s64)a * a % MOD;
        b >>= 1;
    }
    return res;
}

int Getphi(int n)
{
    int res = n;
    for(int i=2; i*i<=n; i++)
        if(n % i == 0)
        {
            res = res/i*(i-1);
            while(n % i == 0) n /= i;
        }
    if(n != 1) res = res/n*(n-1);
    return res;
}

int Deal(int p)
{
    pn = 0;    phi[0] = p;
    while(p != 1) phi[++pn] = p = Getphi(p);
    phi[++pn] = 1;

    int a = 2;
    for(int i=pn; i>=1; i--)
    {
        if(a >= phi[i]) a = a%phi[i] + phi[i];
        a = (s64)Quickpow(2, a, phi[i-1]);
        if(!a) a = phi[i-1];
    }

    return a % phi[0];
}

int main()
{
    T = get();
    while(T--)
    {
        x = get();
        printf("%d\n", Deal(x));
    }
}